Motivation
Dungeon generators usually let you configure how many rooms do you want to generate, their sizes, how long corridors do you want, etc. If you want to control the structure of generated dungeons, they sometimes let you specify how sparse or dense should the dungeons be or how many corridors should be connected to each room. And based on that configuration, they generate a random dungeon layout.
For me, the biggest advantage of such generators is that the setup is usually very simple, and you can start generating your dungeons literally after a few minutes. Another advantage is that these algorithms can often quickly generate layouts consisting of tens or even hundreds of rooms because there are not that many constraints on the structure of the dungeon so the process of finding a suitable dungeon is quite simple. These dungeon generators are perfectly suitable for the majority of games.
The main goal of this dungeon generator is to give game designers complete control over the structure of generated layouts. This is achieved by specifying so-called level (connectivity) graphs which describe how many rooms you want to generate and how they should be connected to one another. Moreover, the look of individual rooms is controlled by so-called room templates.
Through the level graph, a game designer can easily affect the flow of gameplay. Do you want a single main path to a boss room with some optional side paths? Simply start with a path graph and then pick some nodes where the player can choose to either follow the main path or explore a side path with possible treasures and/or monsters waiting for him or her. Do you want a shortcut? Simply choose two nodes in the graph and add a shorter path that connects them. The possibilities are endless.
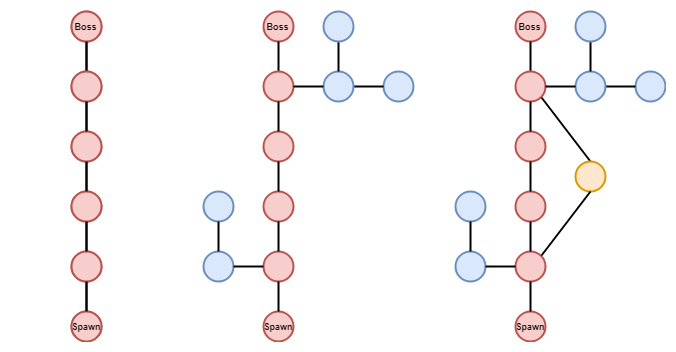
The price for all of this is the performance of the algorithm. The most difficult thing is laying out rooms that are part of a cycle in the level graph. And even though the algorithm is specialized to handle cycles, there is a point where a level graph is simply too complex for the algorithm to handle.